对称、非对称加密技术初探

一、对称加密

对称加密简介

对称加密算法所用到的基本的方法是：代换和置换。简单来说：（以早期的加密方式举例）
- 代换：是将明文字母替换成其他字母、数字或符号的方法
  
  对于明文中的每一个字母，用字母表中k个字母来代替（允许循环，即a可以在z的后面）
  
  例如：如果 k = 3，那么明文中的 a 在密文中就变 d ，b 就变成 e。这里 k 值充当密钥
- 置换：可以说对代换的一种改进，通过并不是通过固定的规则来替换字母，任意字母都可以替换为别的其他字母，但是一一对应的。例如（单表置换加密）：
  
  明文：a b c d e f g
  
  密文：d c h n q i a
  
  以上是早期加密时用的简单的方法，其思想还是通过替换来进行加密的
对称加密过程
常见对称加密算法
- DES
  
  采用64位的分组长度，和56位的密钥长度，将64位的输入经过一系列的变换得到64位的输出。加密解密使用了相同的密钥。
```
* 注： 此算法可以被暴力破解，穷举即可解密，所以不再单纯使用 
```
- 3DES
  
  对DES的改进，使用多个密钥对DES进行三次加密，有些基于Internet的应用已经采纳了这种算法，如：PGP，S/MIME
- AES(高级加密标准)
  
  对DES的再次改进，性能不低于3DES，它的密钥长度为128、192或256位，分组长度为128位
- Blowfish算法
  
  一种可变密钥长度的分组加密算法，分组长度64位。迄今为止，该算法的安全性还没有受到挑战
- RC5算法
  
  参数可变的分组加密算法，此算法使用了三种运算：异或、加、循环

二、非对称加密

基于数学函数的算法，而不再是基于代换和置换技术，公钥加密算法是非对称的

根据加密算法和加密密钥是推不出解密密钥的

关于公钥、私钥

正确理解：

公钥是用于 加密 和 认证 的
私钥是用于 解密 和 签名 的

* 这两个密钥，任意一个都可以用来加密，另一个用来解密
* 公钥是公开的

非对称加密过程
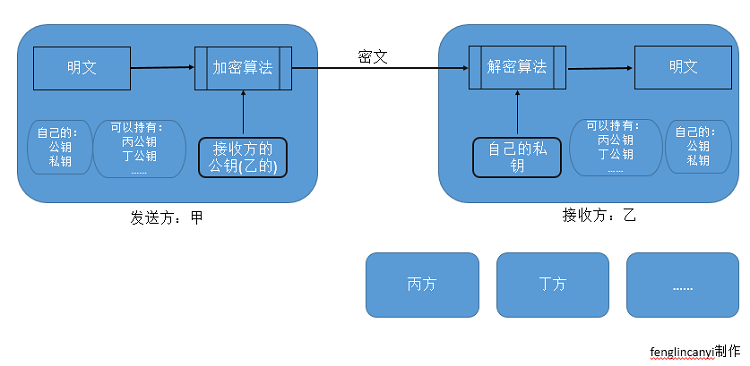
RSA简介

第一个能用于数据加密也能用于数字签名的算法，RSA是一种分组密码
- 易于理解和操作，但安全性一直没有得到理论上的证明
- RSA的加密和解密时间是DES的上百倍，效率较低
  
  选取密钥的过程：
  
  (1). 选取两个大质数 p, q. 质数值越大，破解 RSA 就越困难，进行加密和解密的时间就越长
  (2). 计算 n = p q, z = (p-1) (q-1)
  (3). 选取 e < n, 且与 z 互质（e 和 z没有公约数）
  (4). 找到数 d, 满足 ed - 1 被 z 整除（ ((e * d) - 1) % n) == 0 ）
  (5). 公钥：（n, e）; 私钥：（n, d）
  
  加密、解密过程：
  
  (1). 甲方（发送方）：发送 m (发送数)，m < n,
  (2). 发送时，用乙方（接收方）的公钥加密：密文 c = m^e % n
  (3). 乙方：解密用自己的私钥，得到明文 m = c^d % n
其他非对称加密算法
- ElGamal算法：基于公钥密码体制和椭圆曲线加密体系，既能用于数据加密，又能用于数字签名
- 背包加密算法：基于背包算法，但是大多数一次背包体制均被破译了，因此很少有人使用它

散列(哈希)函数

是公开的函数，可以将任意长的串映射成一个固定长度的串，Hash值由下面的函数 H 生成：
```
h = H (M)

M: 变长的消息，H(M)是定长的 Hash值
```
常见的散列函数有： MD5，SHA-1
- MD5：
  
  有广泛的应用，如在 Java API 中就有体现，但也不安全，有人专门将大量的明文和密文收集起来存至数据库中，用于暴力破解MD5。所以实际使用时，需 “加盐”
- SHA-1:
  
  在Linux系统、Git中都有广泛的使用，它的原理类似于 MD4(MD5的前身)。
  
  说明： MD5 和 SHA-1被好多人称为加密算法，其实这两个散列函数，是用于散列获得消息摘要的，严格来说，应该叫做 消息摘要算法
数字签名

签名是用来验证发送方的身份和数据的完整性(数据是否被第三方篡改)的

签名分为：
- 普通数字签名（如：RSA，DES）
- 特殊数字签名（如：有盲签名，代理签名）
  
  数字签名过程：
  
  (1). 发送方生成一对公钥和私钥，将自己的公钥发送给接收方
  (2). 发送方将要发送的消息 msg, 进行散列(MD5或者SHA-1)，得到消息摘要
  (3). 发送方将消息摘要用自己的私钥加密，加密后的信息就是数字签名
  (4). 发送方将数字签名附在要发送的消息 msg’ (是通过接收方的公钥加密后的) 的后面，再一起发送至接收方
  数字签名的验证过程：
  
  (1). 接收方收到消息后，对消息 msg’ 使用自己的私钥进行解密得到 msg
  (2). 接收方对数字签名使用发送方的公钥解密，得到消息摘要(之前是由消息经过散列得到)
  (3). 接收方使用相同的散列函数(散列函数也是公开的)对 msg 进行散列，再计算得到一个消息摘要
  (4). 接收方对比着两个消息摘要即可判断出消息的完整性
  
  身份的正确性：可通过使用公钥能否解开数字签名来判断
  
  数据的完整性：可通过对比两个消息摘要是否相同来判断

对称、非对称加密技术初探

一、对称加密

二、非对称加密

谢谢打赏